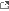29
Dispatch → Meta → Reference
Fractal nerdery
Here's a sequence of images I made of the Mandelbrot set. Each one is made by zooming in on a portion of the previous one.We start with the whole set.
Now we head for an area a little bit south of the point where the two main black segments come together.
It's hard to see much detail, so let's pick out just one of the spiral structures from the left hand side.
Nice, but what are those tiny black objects?
They're copies of the original Mandelbrot set. Let's do with this one what we did with the full size one and zoom in on the area where the two main segments come together.
It's quite similar to before, but this time there's that blue stuff in the space between. Let's zoom in on a bit of that.
It's all very blue... except for those pink bits. What's going on there?
The spirals are pretty, but there's also a little island in the centre of this region. We'll go there next.
By now, it should be no surprise what the little black detail is.
This time, rather than heading to the mini-Mandelbrot we'll go to one of the golden spirals on the edge of the mandala...
... and another level down on the left for a better colour contrast. I'd like to stress that although the result looks just a little bit closer, the next image is about 0.00001 of the area of the last one - the green centre top right isn't the green centre in the image above, it's the centre of just one of the tiny spirals in the chain on the left.
And as far as I know from here every zoom in will look much the same. It never comes to an end, though our computing power does. That last image is at a zoom factor of about 10 trillion.
So apart from pretty pictures, what were we looking at here?
Every pixel of the image represents a number. Ordinarily, numbers are spaced out along a 1D line rather than a 2D plane, but these are complex numbers.
Now that we're equipped with i negative numbers do have square roots, but we have to deal in complex numbers. A complex number has a real part and an imaginary part. For example, 2 + 3i is a complex number with real part 2 and imaginary part 3. Because i is defined by the fact that i x i = -1 we can do arithmetic with complex numbers. For example (2 + 3i) + (1 - i) = 3 + 2i while (2 + 3i) x (1 - i) = 5 + i. It's just a matter of multiplying out the brackets like you did at high school.
There are various mathematical reasons why complex numbers are the place we ought to be doing mathematical stuff because things work out there in a way they don't using real numbers alone. There also are practical applications, it isn't just abstraction for the hell of it.
Anyway, the point here is that if you think of the image as a graph or coordinate system (with invisible axes) then the point (x,y) represents the complex number x + yi, and that's how each point matches a number.
We take the number that represents the point and we square it (multiply it by itself). That's stage 1. For stage 2 we square stage 1 and then add the original number. For stage 3, square stage 2 and add the original number. And so on...
Examples are good. Let's consider the point representing 0.5.
Stage 1 = 0.5 x 0.5 = 0.25
Stage 2 = 0.25 x 0.25 + 0.5 = 0.5625
Stage 3 = 0.5626 x 0.5625 + 0.5 = 0.81640625
Stage 4 = 1.167 (ish)
Stage 5 = 1.861 (ish)
Stage 6 = 3.96
Stage 7 = 16.3
and the numbers now get very large very quickly.
Next up, the point representing -0.1
Stage 1 = -0.1 x -0.1= 0.01
Stage 2 = 0.01 x 0.01 - 0.01 = - 0.0999
Stage 3 = -0.0900
Stage 4 = -0.0919
Stage 5 = -0.0919
and the sequence stabilises.
For any number, the sequence generated either stabilises or go whizzing off to infinity. The numbers for which is stabilises are the members of the Mandelbrot set, and they are black on the image. The numbers for which it goes whizzing off are not part of the the Mandelbrot set and they get assigned a different colour based on how fast the whizzing goes.
The image is calculated by doing this for every pixel.
And this is weird because...
There's no reason to think that a simple process like this should give rise to such a ridiculously complicated outcome. Normally if you divide numbers into a set for which something happens and a set for which it doesn't you'll divide your plane up into two sections with a curve or straight line between them, or perhaps be looking at the inside and the outside of a circle.
In the last image, the 10 trillion zoom factor meant that all the numbers involved would have been identical for about the first 12 decimal places. Finding that kind of structure in such tiny differences is completely mind-bending.
Chaos theory
Chaos theory, or more properly the theory of chaotic dynamic systems, is about sensitivity to initial conditions. If you throw a ball at a window then there's a ball speed above which the window will break and below which it won't. Very limited sensitivity to initial conditions. But if you let an iron pendulum swing freely over two magnets then moving its starting point by a fraction of a millimetre can cause it to come to rest over a different magnet... or not. The system is completely unpredictable.
There's a cliche about the butterfly effect - a butterfly in South America flaps its wings and the turbulence changes the course of a European hurricane. Much of chaos theory emerged out of weather forecasting, a dynamic system very sensitive to its starting conditions. Mandelbrot images became associated with the theory because of the way they embody that kind of sensitivity, and the bizarre presence of intricately detailed structure behind apparent randomness. Plus they look cool.
Software
I made these images using freeware from www.mandel.org.uk. The is only one dive from the top to a high level of zoom, a limitless number is possible.